Fixed Point Mathematics for Z180
This fixed point mathematics library will work on the many processors that implement the Z180/64180 instruction set. It provides 32 bit multiplication, division, sine, cosine and arctangent functions. It is coded entirely in assembly and has been throughly tested.
Introduction
In the Spring Term of 2002, I worked on an embedded system for a computer science course called 'MCP': Microcomputer Project. The embedded system was able to determine its position within the hardware lab where it was built. It did this by measuring the relative angles of a number of beacons and then applying some mathematical formulas.
When the project was beginning, I believed that the way to make the best project in the class was to write the best software for my machine. The final accuracy and speed of the device, which would be competing with similar systems made by other people doing the course, would depend mainly on the quality of the software that powered it.
So I put a lot of effort into writing a library of high accuracy mathematical functions for this embedded device, which ran on a Hitachi 64180 processor (compatible with the Z180, and *mostly* compatible with the famous Z80 processor). I wouldn't have got any credit for copying someone else's functions: they had to be written by me, and they had to be written in assembly code. I wrote this library over a period of several weeks and tested it throughly using automatic tests in an emulator and on the actual system.
Unfortunately, despite my efforts, the accuracy of the system really depended on the accuracy of the hardware that worked out the beacon angles. Although my system was one of the few that worked, and had a very high level of accuracy in theory, in actuality the sub-par construction of the scanner meant that it produced fairly poor results. It finished 4th (out of about 30).
But, as I have said, this was not the fault of the software. In the hope that the mathematics library may be of some use to someone else, I am releasing it generally.
This may be useful to anyone writing software for the Z180, 64180, or processors based on them. These libraries are not small, but they are fast and accurate, and written entirely in assembler. They have been throughly tested and some optimisation has been done by profiling.
In particular, this code may be useful to students working on the MCP project at York. If you find that you need mathematics routines, but don't have time to write them yourself, then use mine and credit me in your report (you're allowed to do that, or at least you were when I did it). The code will assemble unchanged in the H180 assembler used at York.
Files
- The library itself
- The library as part of a
large application (MCP project).
Please do be aware that the entire application will only work on very specific hardware. It is included here only as an example: it is almost totally useless in all other respects!
(The code is provided under the terms of the GNU GPL).
Notes about the code
The library comes as a bunch of .s assembly source files. You don't strictly need them all, there's an order of dependencies which you can find here. But it doesn't hurt to have the whole lot.
You can call any of the procedures on the dependency diagram from your own code. All you need to do is understand the calling convention which I will attempt to explain shortly. The procedures and functions are all register preserving (the registers are saved by the procedure, so you don't need to put them on the stack before calling). No global variables are used at any time. Parameters are passed on the stack.
Before the code will work, you will need to edit the exception handling code (search for divide_by_zero_error, divide_overflow and multiply_overflow). It prints a string to a serial port using some other code which is not part of the library: you should probably make it call your own output functions if you have any.
If you aren't using the same assembler as me, you may also have to do some editing to get the syntax right. The assembler used here is called 'h180' and it is (or was) free software. Unfortunately I don't have a link to it.
If you are trying to get this code to work on a Z80, then you will need to find every instance of the MLT (multiply) instruction, which is not supported on the Z80, and replace it with a call to lightweight_software_multiply_b_and_c which you can find in lightweight-multiplier.s. This is a (slow) 8 bit software multiplier which will allow you to run the code on an original Z80.
Fixed point number format
The fixed point number format is 8.24 bits: There are 8 bits to the left of the decimal point, and 24 to the right of it. This allows any number from -127 to +127 to be represented. Negative numbers are stored in 2's complement form. The following table illustrates how decimal numbers are represented in this way. Note that the most significant byte of the fixed point number is actually on the right hand side, since the 64180 is a little endian processor
| Decimal number | Fixed point number (4 Bytes in Hex) |
|---|---|
| 0 | 00 00 00 00 |
| 6 | 00 00 00 06 |
| -6 | FF FF FF FA |
| 6.5 | 00 00 80 06 |
| 6.25 | 00 00 40 06 |
| 1/256 | 00 00 01 00 |
| 1/65536 | 00 01 00 00 |
Calling convention
From the start, the project had adopted a "pass by stack" calling convention for functions and procedures. Originally, it was believed that the best way to pass fixed point numbers to a mathematical function was by pointer. So, for example, the multiply_fp function accepted two pointers. Each pointer referred to a fixed point number. multiply_fp would dereference both pointers, perform the multiplication, and store the result at the second of the two pointers. This was believed for some time to be ideal: there was no need to copy fixed point numbers onto the stack so that a function could use them. Instead, a single pointer was all that was required.
However, this proved to be far from ideal when the time came to apply the mathematical functions to more complex tasks. Even linear interpolation proved to be a substantial challenge: it is simple compared to the application of the formula for q1. It was difficult to manage the pointers required: in fact, this was just as hard as managing the numbers themselves. Code to do this generally involved adding and subtracting numbers from pointers to move them to the correct places. It was difficult to follow and tedious to write, and bugs could be introduced easily. For this reason, this calling convention was dropped halfway through the project and all the fixed point mathematical functions were rewritten to follow a new calling convention, designed specifically to overcome this particular problem while providing the same facilities to the programmer. The new system was such an improvement, and saved so much time in the end, that the rewrite was quite justifiable.
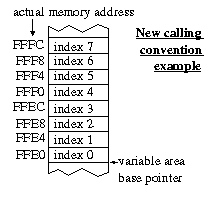 The new design standardised the calling convention for all fixed point functions. The caller must push a pointer to the start of the "variable area" to be used, and then push two indexes for the locations of the variables to be used by the function, which are within that area. The fixed point function then uses a subroutine named lightweight_marshal_parameters_arity_2 (or _arity_1 for single parameter functions) to convert the indexes and variable area base pointer to the actual pointers to variables within the variable area. The upshot of this is that all functions can be called with the same variable area pointer, but with different indexes to refer to different variables within the area. The calculation of the actual pointers to the variables is done by the fixed point function, and not by the caller, making the use of these functions far easier. The diagram on the right helps to illustrate this. The variables at index 1 and index 2 could be multiplied by calling multiply_fp with the variable area based pointer (FFE0) and indexes 1 and 2.
The new design standardised the calling convention for all fixed point functions. The caller must push a pointer to the start of the "variable area" to be used, and then push two indexes for the locations of the variables to be used by the function, which are within that area. The fixed point function then uses a subroutine named lightweight_marshal_parameters_arity_2 (or _arity_1 for single parameter functions) to convert the indexes and variable area base pointer to the actual pointers to variables within the variable area. The upshot of this is that all functions can be called with the same variable area pointer, but with different indexes to refer to different variables within the area. The calculation of the actual pointers to the variables is done by the fixed point function, and not by the caller, making the use of these functions far easier. The diagram on the right helps to illustrate this. The variables at index 1 and index 2 could be multiplied by calling multiply_fp with the variable area based pointer (FFE0) and indexes 1 and 2.
Here is a short code example to show how two numbers might be multiplied.
# This is where we're going to keep our variables.
# It's a space of size 64 bytes. That's enough for
# 16 variables. (4 * 16 = 64)
variable_area:
.space 64
# This subroutine will calculate 6 * 7.
what_is_6_times_7:
# Load the fixed point value 6 into the first space in the
# first space in the variable area.
# (6 is 0x00000006 in fixed point)
ld hl,0
ld (variable_area),hl
ld hl,0x0600
ld (variable_area + 2),hl
# And load 7 into the space after it.
ld hl,0
ld (variable_area + 4),hl
ld hl,0x0700
ld (variable_area + 6),hl
# Now, put the start of the variable area on the stack.
ld hl,variable_area
push hl
# Now the variable area base pointer is on the stack.
# Put the indexes of the two numbers to be multiplied on
# the stack too.
ld hl,0x0100 # multiply numbers at indexes 0 and 1,
# and store the result at index 1.
push hl
# do the multiplication
call multiply_fp
# remove indexes and the base pointer from the stack
pop hl
pop hl
# Now the result (42) is at index 1 in the variable area,
# i.e. at variable_area + 4.